(Δεν αναφέρεται στο σχολικό βιβλίο. Σχετίζεται με: Κεφ. 1ο, §1.7 σελ. 18-22)
Τις διάφορες μορφές ΚΠΔ, τις διακρίνουμε με κριτήριο το Κόστος ευκαιρίας του αγαθού. Βασικές μορφές θεωρούνται οι ΚΠΔ αυξανόμενου και σταθερού αντίστοιχα κόστους ευκαιρίας. Για άλλες πιθανές “μορφές ΚΠΔ”, δες τις ειδικές ΚΠΔ.
Για όλες τις ΚΠΔ αυξανόμενου κόστους, που αποτελούν τη συνηθέστερη μορφή ΚΠΔ ισχύει:
Α. Το κόστος ευκαιρίας είναι αυξανόμενο
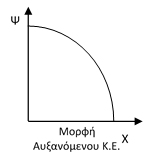
Β. Η καμπύλη στρέφει τα κοίλα προς τα μέσα. Η συγκεκριμένη καμπύλη παραγωγικών δυνατοτήτων έχει συνήθως απροσδιόριστη εξίσωση, αφού δεν είμαστε ποτέ βέβαιοι για την ακριβή μορφή της.
Γ. Επίσης η παραγωγικότητα της εργασίας δεν παραμένει σταθερή και για τα δύο αγαθά.
Δ. Η οικονομική ερμηνεία της είναι ότι οι συντελεστές παραγωγής δεν είναι εξίσου κατάλληλοι για την παραγωγή και των δύο αγαθών. Δηλαδή όσο αποσπώνται συντελεστές από την παραγωγή του ενός αγαθού τόσο περισσότερες μονάδες του άλλου αγαθού θυσιάζονται.
Το παράδειγμα 1 παρουσιάζει μια καμπύλη αυξανόμενου κόστους ευκαιρίας.
Σημείωση: Δεν είναι τυχαίο ότι συνήθως αναφέρονται τα αγαθά όπλα και τρόφιμα, τα οποία έχουν μεγάλη διαφορά στην παραγωγική τους διαδικασία και οι συντελεστές που χρησιμοποιούνται είναι πολύ διαφορετικοί.
2. ΚΠΔ Σταθερού Κ.Ε.
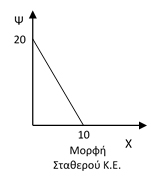
Για παράδειγμα εδώ θα μπορούσαμε να είχαμε μια μικρή βιοτεχνία ρούχων η οποία παράγει δύο αγαθά, τα παντελόνια (Ψ) και τα πουκάμισα (Χ), χρησιμοποιώντας 10 εργάτες, ως μοναδικό συντελεστή παραγωγής, και γνωρίζουμε ότι κάθε εργάτης μπορεί να παράγει 2 παντελόνια (Ψ) ή 1 πουκάμισο (Χ).
Σύμφωνα με το παράδειγμα θα μπορούσα να κατασκευάσω την διπλανή ΚΠΔ.
Θα ισχύει για όλες τις ΚΠΔ σταθερού κόστους:
Α. Το Κόστος Ευκαιρίας θα είναι σταθερό σ’ όλους τους συνδυασμούς της ΚΠΔ.
![\[KE_X = \frac{\Delta\Psi =20}{\Delta X =10}= 2 \]](https://ceterisparibus.gr/app/ql-cache/quicklatex.com-dcae71e11bb898250daf5e48accb4441_l3.png "Rendered by QuickLaTeX.com")
και
![\[KE_\Psi = \frac{\Delta X =10}{\Delta\Psi =20 }= 0,5 \]](https://ceterisparibus.gr/app/ql-cache/quicklatex.com-aa776117ffb5065b1b7ea0ea41f7acaa_l3.png "Rendered by QuickLaTeX.com")
Β. Εάν το κόστος είναι σταθερό τότε η ΚΠΔ θα είναι ευθεία, αφού το ΚΕΧ εκφράζει την κλίση της ΚΠΔ, έτσι σταθερή κλίση η ΚΠΔ θα είναι της μορφής:
Ψ = αΧ +β,
Γ. Η Παραγωγικότητα της εργασίας θα είναι σταθερή και για τα δύο αγαθά, αλλά όχι και ίση μεταξύ τους.
Παράδειγμα, εάν η εκφώνηση λέει ότι μια βιοτεχνία ρούχων έχει 10 εργάτες και ο κάθε εργάτης παράγει σταθερά 1 μονάδες από το Χ και 2 μονάδες από το Ψ αγαθό, τότε αναφερόμαστε σε σταθερή παραγωγικότητα της εργασίας και γνωρίζουμε από πριν ότι η ΚΠΔ θα είναι σταθερού κόκόστους ευκαιρίας.
όπου οι παραγωγικότητες για το αγαθό Χ είναι:
![\[ Productivity \hspace{0.5em}of \hspace{0.5em}Labour \hspace{0.5em}X= \frac{Total \hspace{0.5em}Product\hspace{0.5em}X}{Labour\hspace{0.5em} Used} =\frac{10}{10}=1 \]](https://ceterisparibus.gr/app/ql-cache/quicklatex.com-29788d67b96dea554b5f5e0ac97404d1_l3.png "Rendered by QuickLaTeX.com")
ενώ για το αγαθό Ψ είναι:
![\[ Productivity \hspace{0.5em}of \hspace{0.5em}Labour \hspace{0.5em}Ψ= \frac{Total \hspace{0.5em}Product\hspace{0.5em}Ψ}{Labour\hspace{0.5em} Used} =\frac{20}{10}=2 \]](https://ceterisparibus.gr/app/ql-cache/quicklatex.com-f4f92452948d8ec606560f3cb28dc92c_l3.png "Rendered by QuickLaTeX.com")
Δ. Η οικονομική ερμηνεία της ΚΠΔ, είναι ότι οι συντελεστές παραγωγής είναι ικανοί να παράγουν ποσότητες από ένα αγαθό, ως προς μια σταθερή αναλογία θυσία του άλλου.
Σημείωση: Δεν είναι τυχαίο στο παράδειγμα ότι αναφέρθηκαν τα αγαθά παντελόνια και πουκάμισα, τα οποία έχουν μικρή διαφορά στην παραγωγική τους διαδικασία και οι συντελεστές που χρησιμοποιούνται είναι παρόμοιοι.
Τα υπόλοιπα ανοιχτά σημεία της θεωρίας για όλους τους επισκέπτες της σελίδας είναι τα παρακάτω:
Β2α. Καμπύλη Παραγωγικών Δυνατοτήτων – Κ.Π.Δ.
Μπορώ να δω όλο το υλικό;
Προτού κάνεις εγγραφή θες να είσαι βέβαιος ότι το “Ceteris Paribus” έχει αρκετό υλικό και σε υψηλό επίπεδο;
Ναι, μπορείς.
Επικοινώνησε με την σελίδα και μπορείς να πάρεις ένα κωδικό που θα ισχύει για περιορισμένο χρόνο και θα σου δίνει πρόσβαση σ΄ όλο το υλικό της ιστοσελίδας “Ceteris Paribus”.
Έτσι θα μπορέσεις να ξεφυλλίσεις όλη τη ΘΕΩΡΙΑ, τις ΑΣΚΗΣΕΙΣ, τις ΕΡΩΤΗΣΕΙΣ όλων των τύπων, αλλά και να δεις τα ΒΙΝΤΕΟ, τα οποία περιλαμβάνονται μόνο στην ιστοσελίδα, αλλά όχι στο κανάλι του “Ceteris Paribus” στο YouTube.
Πάμε εγγραφή!
Είμαι έτοιμος. Θέλω να κάνω συνδρομή τώρα.
Πάμε για εγγραφή!